Skip to main content
Facts

Fermat’s great theorem

By 9. September 2016November 30th, 2020No Comments

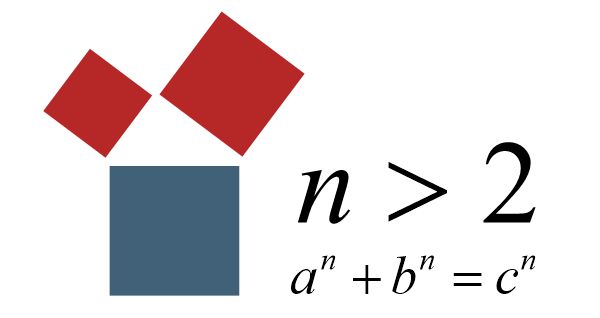
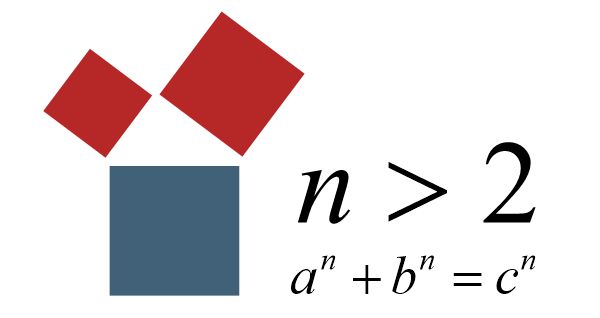
Facts

Fermat's great theorem

2016-09-09

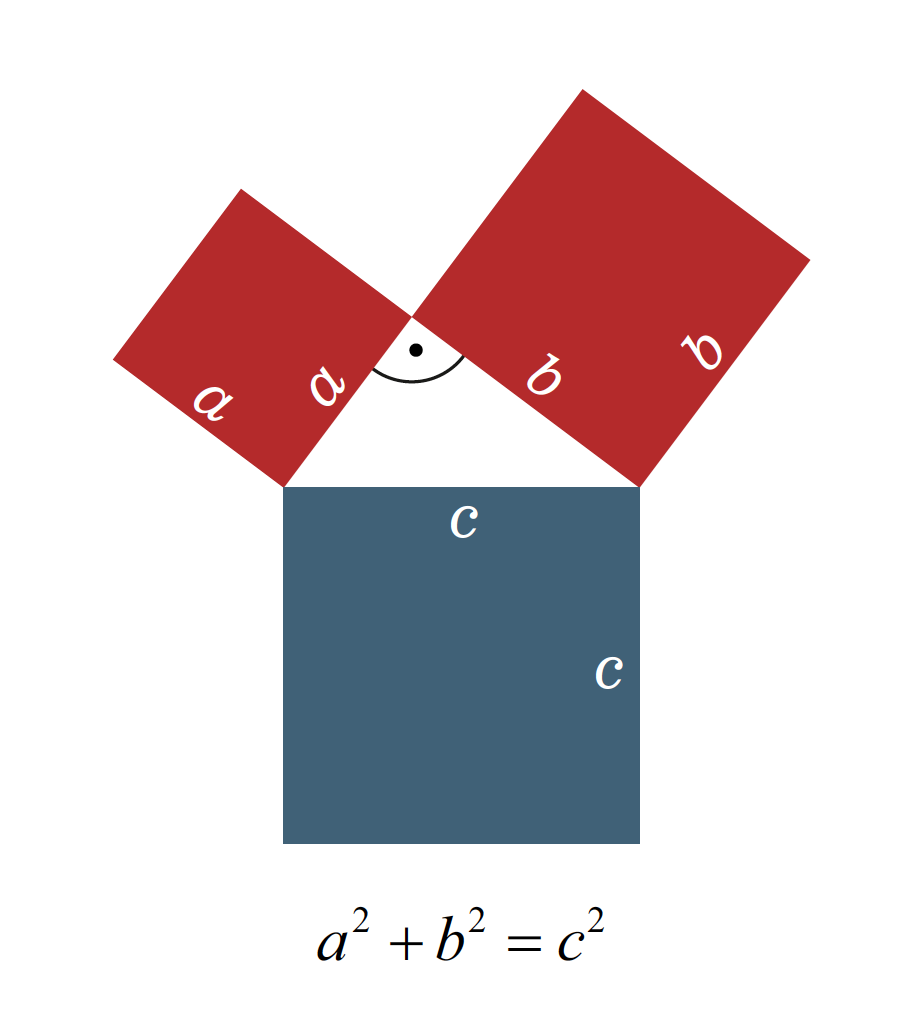
The theorem of Pythagoras is known by practically every schoolchild. The mathematical theorem says that in a right-angled triangle the sum of the areas of the squares of the cathets is equal to the area of the hypotenuse square:

If the lengths of all sides of a right triangle are integer numbers, it is called a Pythagorean triple. The smallest and probably best known Pythagorean triple is a right-angled triangle with

Among the Pythagoreans such triples were especially revered, because they correspond to harmonic relationships. These relationships were already known to the Babylonians around 1600 BC. They were used to construct right angles and measure land.

For n = 2 in the equation

surprisingly there are infinitely many solutions with natural numbers, i.e. Pythagorean triples.

Pierre de Fermat claimed more than 350 years ago that for n > 2 there are no integer solutions for a, b and c. The ingenious leisure mathematician missed the proof for this. In his edition of the Arithmetica of Diophantos of Alexandria he merely wrote

“I have discovered a truly wonderful proof for this, but this margin here is too narrow to grasp it.”

Such a statement made this problem of number theory a challenge for many mathematicians, but after many mistakes but also partial successes, for example in 1738 by Leonhard Euler for n = 4, it was not until 1993 by Andrew Wiles at the Isaac Newton Institute in Cambridge that it was put to rest. Fermat was right, the margin was indeed too narrow. Wiles’ proof, with all the secondary arguments, covered almost 100 pages. With this proof, Fermat’s conjecture has become Fermat’s great theorem.

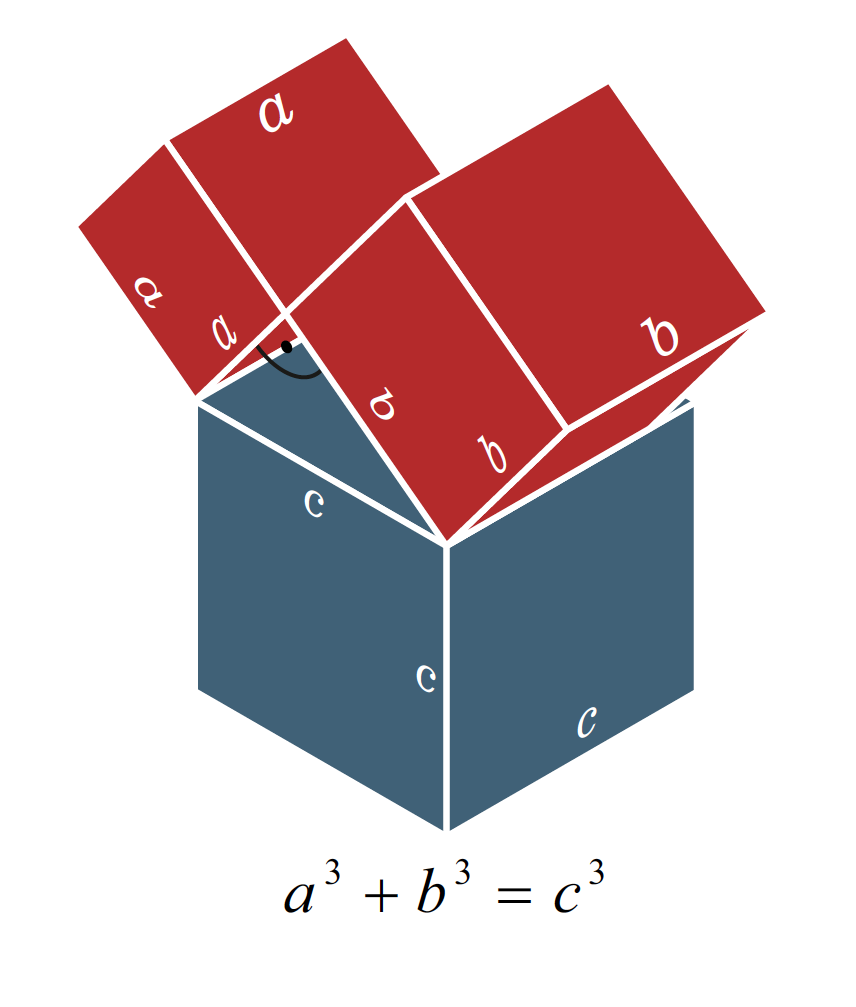
As well known and understandable as Pythagoras’ theorem is, it is difficult to develop an idea for n > 3. The representability supports the comprehensibility of facts significantly.

With n = 2 we have no problems with the well-known Pythagorean theorem.

We can also illustrate n = 3 very well on the basis of n = 2.

All other powers fail because of the visual representability, due to the lack of a real equivalent.

Let us not despair of the apparently unattainable,
but simply enjoy what is possible …
… for example the …

Illustrations on the subject with the Corel DESIGNER
  • Right-angled triangle, if the cathets are known
    create a rectangle with correct dimensions using the docker Coordinates
    convert the rectangle into a curve and delete a node
  • Right-angled triangle, if the hypotenuse is known
    Create a triangle with a Multi-Point line and snap over the diameter (= hypotenuse) of a circle (= theorem of Thales)
  • Squares of cathets and hypotenuses
    3-point rectangle tool + Ctrl (square)
  • n = 3
    Docker Transform / Project
    Extrusion tool + Ctrl
  • Equations
    Equation Editor