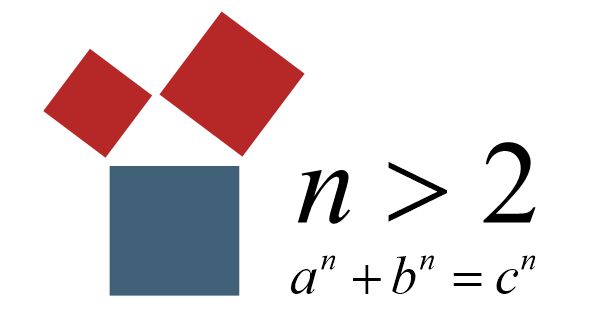
Fakten
Fermats großer Satz
09.09.2016
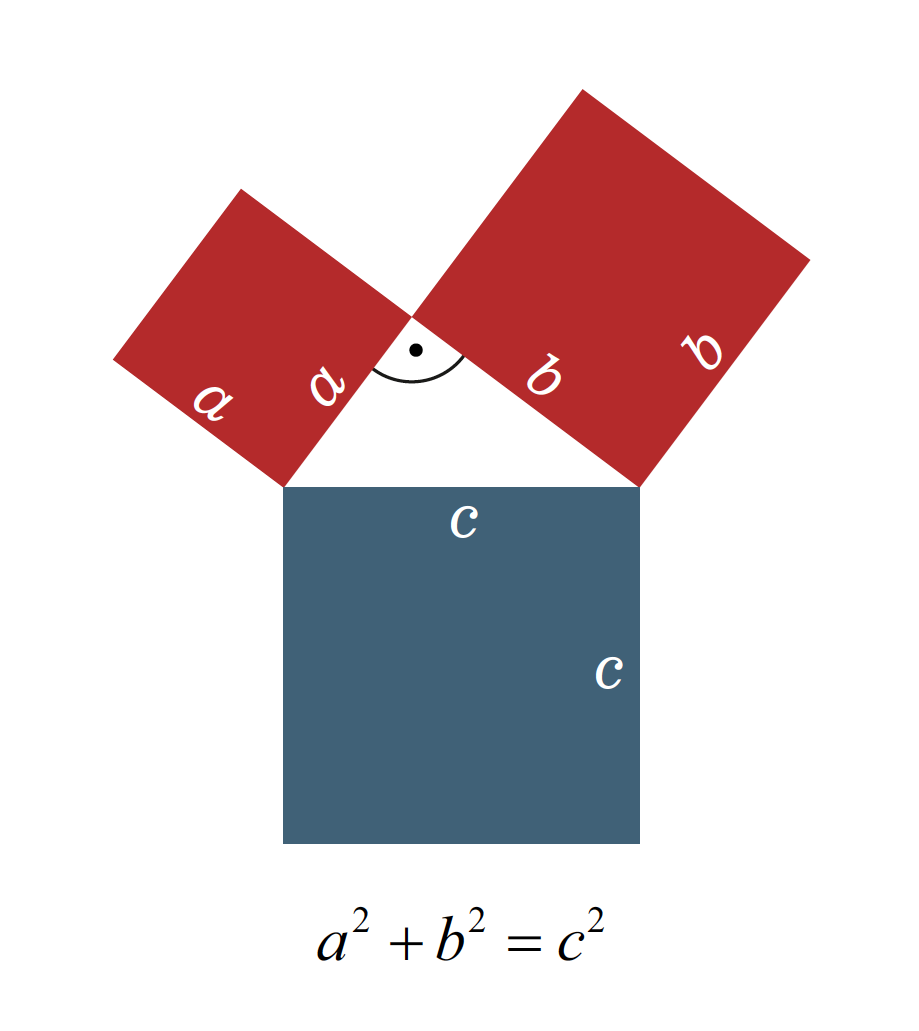
Den Satz des Pythagoras kennt praktisch jedes Schulkind. Der mathematische Satz sagt aus, dass in einem rechtwinkligen Dreieck die Summe der Flächeninhalte der Kathetenquadrate gleich dem Flächeninhalt des Hypotenusenquadrates ist:
Sind in einem rechtwinkligen Dreieck die Längen aller Seiten ganzzahlig, spricht man von einem pythagoreischen Tripel. Das kleinste und wohl auch bekannteste pythagoreische Tripel ist ein rechtwinkliges Dreieck mit
Bei den Pythagoreern wurden solche Tripel besonders verehrt, da sie harmonischen Verhältnissen entsprechen. Diese Zusammenhänge waren auch schon den Babyloniern etwa 1600 v.Chr. bekannt. Damit konnten rechte Winkel konstruiert und Land vermessen werden.
Für n = 2 in der Gleichung
gibt es erstaunlicherweise unendlich viele Lösungen mit natürlichen Zahlen, also pythagoreische Tripel.
Pierre de Fermat behauptete vor über 350 Jahren, dass es für n > 2 keine ganzzahligen Lösungen für a, b und c gibt. Den Beweis dazu blieb der geniale Freizeit-Mathematiker schuldig. In seiner Ausgabe der Arithmetika des Diophantos von Alexandria schrieb er lediglich:
„Ich habe hierfür einen wahrhaft wunderbaren Beweis entdeckt, doch ist dieser Rand hier zu schmal, um ihn zu fassen.“
Durch eine solche Aussage wurde dieses Problem der Zahlentheorie eine Herausforderung für viele Mathematiker, die nach vielen Irrwegen aber auch Teilerfolgen, zum Beispiel 1738 durch Leonhard Euler für n = 4, erst 1993 von Andrew Wiles am Isaac Newton Institute in Cambridge zu den Akten gelegt werden konnte. Fermat hatte Recht, der Rand war tatsächlich zu schmal. Der Beweis von Wiles umfasste mit allem Nebengeplänkel knapp 100 Seiten. Mit diesem Beweis ist aus Fermats Vermutung Fermats großer Satz geworden.
So bekannt und erfassbar der Satz des Pythagoras ist, so schwierig ist es doch eine Vorstellung für n > 3 zu entwickeln. Die Darstellbarkeit unterstützt eben die Verständlichkeit von Sachverhalten erheblich.
Mit n = 2 haben wir mit dem bekannten Satz des Pythagoras keine Probleme.
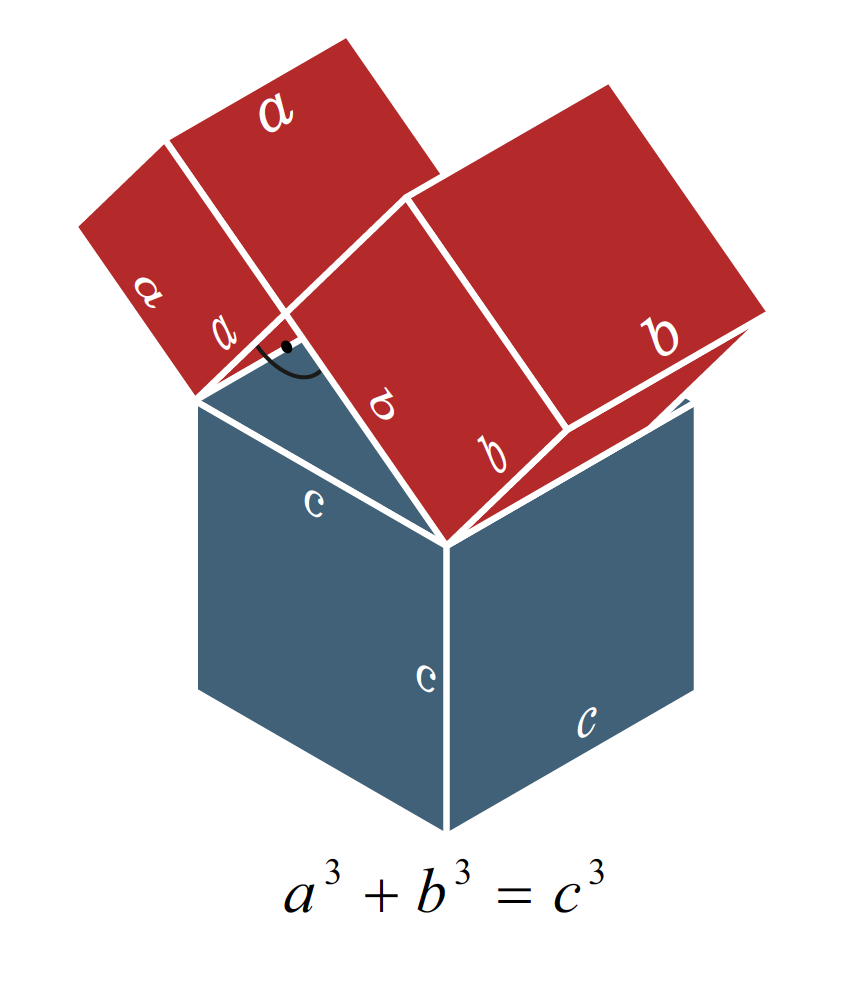
Auch n = 3 können wir auf Basis von n = 2 sehr gut illustrieren.
Alle anderen Potenzen scheitern an der visuellen Darstellbarkeit, durch Fehlen einer realen Entsprechung.
Verzweifeln wir nicht an scheinbar Unerreichbarem,
sondern genießen doch einfach mal das Machbare …
… zum Beispiel die …
Illustrationen zum Thema mit dem Corel DESIGNER
- Rechtwinkliges Dreieck, wenn die Katheten bekannt sind
mit dem Andockfenster Objektkoordinaten ein maßlich korrektes Rechteck erstellen
das Rechteck in eine Kurve konvertieren und einen Knoten löschen - Rechtwinkliges Dreieck, wenn die Hypotenuse bekannt ist
Dreieck mit Mehrpunktlinie und Anziehung über dem Durchmesser (= Hypotenuse) eines Kreise erstellen (= Satz des Thales) - Kathetenquadrate und Hypotenusenquadrat
Hilfsmittel 3-Punkt-Rechteck + Strg (Quadrat) - n = 3
Andockfenster Projizieren
Hilfsmittel Extrusion + Strg - Formeln
Formeleditor